PERCOLATION

• Compressed source code:percolation.rar
• Seminar presentation : percolation.pdf
• TerraME version: 1.3.0

This is a simulation of mathematical percolation theory.

Simulate pouring fluid onto the top surface where the fluid will enter any empty cell it has access to.

The fluid does not move beyond the horizontal constraints of the grid. The fluid may move down within the confines of the grid of cells.

If the fluid reaches a bottom cell that has a missing bottom wall then the fluid can be said to 'drip' out the bottom at that point.

Percolation is a geometric problem that has been extensively studied using numerous mathematical techniques, and plays an important role in statistical mechanics.

Percolation theory is applied in many fields, such as, civil engineering, water conservancy, environmental protection, geology, petroleum and others.

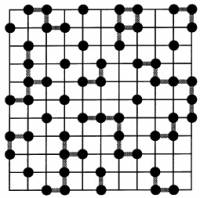
Suppose we have a large array of squares. Let us call the line intersections “sites”, and the segments connecting them “bonds”.

In a square lattice one bond is connected to six nearest neighbor bonds, while a site has only four nearest neighbor sites.

Suppose that each site exists in only two possible states, ‘empty’ or ‘open’ , with open sites being denoted by the presence of a large dot on the intersection, and suppose further that whether a site is open or empty is random and independent of its neighbors.

A bond is assumed to exist between each pair of nearest neighbor sites on the lattice.

If half the sites are open, we see that open sites tend to group into clusters of many shapes and sizes.

We can refer to these clusters by their size, i.e., a single open site with no immediate open neighbors is a 1 cluster; two adjacent open sites with no open neighbors form a 2 cluster, and so on.

-Parameters:

HOLLOW = 1

SPILL = 2

OIL = 3

SAND = 4

SPILL2 = 5

- With the “legend” button, the attributes of the parameters can be changed.

- With the “grid” button. the grids in the area can be showed.

- With the “In” “Out” “Pan” Button, the area can be zoomed in/out or scanned.

-The Volume is the area which is polluted.

-The Path is how the pollutants spread in the soil.

The model can be run as long as you like; if the spill reaches the bottom of the view, the bottom row of squares is moved to the top, and the model continues to run from where it left off, starting at the top of the view.

- The soil cells in the model are independent from each other. What if there are some cells connected to each other? Such as some “open” cells are next to each other closely?

- Try to calculate the running time of different number of grids.

- Currently the order of the grids in this model is regular(the opened ones and the closed ones are ranged one by one).Please try the random order of the grids and execute the model.

- Support cellular automata models running in 2D cell spaces.

- Provides an interface to TerraLib geographical database

- Allowing models direct access to geospatial data.

Fire-Spreading-Model

http://www.terralab.ufop.br/dokuwiki/doku.php?id=terralab:modelo:fire:index

Wilensky, U. (1998). NetLogo Percolation model. http://ccl.northwestern.edu/netlogo/models/Percolation. Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston, IL.

Wilensky, U. (1999). NetLogo. http://ccl.northwestern.edu/netlogo/. Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston, IL.

P. H. L. Martins and J. A. Plascak(2003).Percolation on two- and three-dimensional lattices Phys. Rev. E 67, 046119

J.J. Vaccaro(2007). A Deep Percolation Model for Estimating Ground-Water Recharge: Documentation of Modules for the Modular Modeling System of the U.S. Geological Survey Scientific Investigations Report 2006–5318

Duncan Callaway, M. E. J. Newman, Steven H. Strogatz, and Duncan J. Watts, Network ro- bustness and fragility: Percolation on random graphs, arXiv:cond-mat/0007300, Oct. 2000.