2D DAISY WORLD

• Compressed source code: daisyworld.zip
• Seminar presentation : daisyworldpresentation.pdf
• TerraME version: 1.3.0

This model is to represent the Gaia theory by Lovelock in 1960's which is about life on earth, how it appear and evolve and how the organisms life has a role in earth's climate by interacting with the surroundings like (solid earth, atmosphere, oceans) in a way that can keep and maintain life on earth .

The daisyworld model which was represented by (Watson and Lovelock, 1983) can be applied to understand the mechanisms in which feedback loops can balance and control the climate. The model is represented as a world that is populated by two type of daisies: White daisies and Black daisies. Both have an optimum temperature to grow and they can only reproduce in a range of temperatures. White daisies have low albedo, which means they reflect light and cool the area around them, and black daisies have high albedo, which mean they absorb light and warm the area around them. So the area around the world where black daisies were abundant the temperatures were raised, and where the white daisies were abundant the temperatures were lowered.

The model will allow us to investigate how life on earth may lead to a stable climate.

We have three type of cells: White daisies, Black daisies and soil, with a given albedo for each of them.

The cells are placed randomly in the cellular space depending on the given percentage of soil and white daisies, in the remaining there are placed black daisies. Each of them is given with a random initial age, to control the population of daisies, because when they are old (given age) they die.

Each cell is also given a random initial value for soil heat between the range of possible values of temperature.

Each time step for CA, the temperature will be calculated as follows: Each cell temperature will be calculated according to the daisy albedo and the previous temperature, also the mean neighbours temperature is calculated and this value is used to calculate the mean between the temperature from the cell itself and the mean of the neighbours.

If there is an empty cell with a daisy as neighbour, and the conditions for reproduction are fulfilled, a new daisy will be born in the empty cell.

The conditions for reproduction are that the daisy's ground has to be inside the range of temperatures, and if it is in the given perfect temperature to reproduce it will have 100 % of chances to reproduce, and less chances the further it is from the perfect temperature. The new born daisy will be the same type as the maximum neighbourhood type (black or white).

The daisies will die on a certain (given) age.

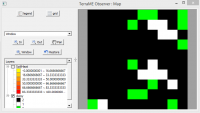
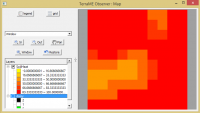
When running the model, it will show a graph for the daisies population and a map with the cells.

This are the parameters which should be set at the beginning:

EMPTY_PROPORTION = 0.7 – 70% of cells will start empty

WHITE_PROPORTION = 0.6 – from the remaining ones 60 % will be white

MIN_TEMP = 0 – This is the minimum temperature possible in the model

MIN_TEMP_REPRODUCE = 40 – This is the minimum temperature where daisies can reproduce

PERFECT_TEMP_REPRODUCE = 50 –With this temperature daisies will reproduce with a probability of 100 %

MAX_TEMP_REPRODUCE = 70 – This is the maximum temperature where daisies can reproduce

MAX_TEMP = 100 – This is the maximum temperature possible in the model

ALBEDO_WHITE = 0.2 – 0-1 How much energy they absorb as heat from sunlight, white reflect light and cool the ground around them

ALBEDO_BLACK = 0.7 – 0-1 How much energy they absorb as heat from sunlight, black absorb light and heat the ground around them

LIFESPAN = 5 –How many timestamps a daisy lives

CSDIMENSION = 50 – Dimension of the cellular space

Notice the graph which shows the total population for each of the cell types (Black, White or Empty)

Also, to see the behaviour of the daisies and the soil heat separately, to make it clear, select only one feature from the map.

If you uncomment the line - - delay_s(1) which is at the end, you will see the model slow down and do a pause of one second between iterations.

If you try with these values, you will see an equilibrium in the flowers and the soil heat:

EMPTY_PROPORTION = 0.5

WHITE_PROPORTION = 0.2

MIN_TEMP = 0

MIN_TEMP_REPRODUCE = 0

PERFECT_TEMP_REPRODUCE = 50

MAX_TEMP_REPRODUCE = 100

MAX_TEMP = 100

LIFESPAN = 10

To extend the model you could add different parameters for the white and black daisies, as the minimum and maximum temperatures to reproduce, in this way you could control the reproduction rate individually for each kind of daisies.

Also, there could be added a new rule to calculate a global temperature, depending on the total number of black and white daisies, and use this global temperature to change the empty spaces temperature.

New types of daisies could be added to the model.

New parameters could be added to control the reproduction rates of the daisies, as soil quality, luminosity or other factors.

This model uses a Cellular Space which creates a Neighbourhood with Von Neumann strategy.

A forEachCell loop is executed each time stamp to search for empty cells, and old daisies that have to die.

Two forEachNeighbor loops are used to search for neighbouring daisies of the empty cells, and to calculate the mean temperature of the neighbours.

Climate change models could be related.

The daisyworld model represented by Watson and Lovelock, 1983

Novak, M. and Wilensky, U. (2006). NetLogo Daisyworld model. http://ccl.northwestern.edu/netlogo/models/Daisyworld. Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston, IL.

Wilensky, U. (1999). NetLogo. http://ccl.northwestern.edu/netlogo/. Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston, IL.